Example of an Onto-Monistic Universally Quantified Argument Form
Consider the following Formally Valid Argument:
∀(.Being.⊗06.Not-Being.),
∀(.Being.⊗06.Nothingness.);
___________________________________________
∴[∀(.Nothingness.≡09.Not-Being.).
The word "Being" is here meant to denote "Monistic Being as a whole."
The Symbology "∀(⊗06)" is here meant to denote: "Everything in the world is Contradictory to:" The TFO "⊗06" is also referred to as: "Exclusive Disjunction."
The Symbology "∀(≡09)" is here meant to denote: "The Subject Set is Equivalent to the Predicate Set."
Note that both the Subject Set as well as the Predicate Set, in this case, are empty.
Universally Quantified (∀) Proposition Types in which Row Four of a Two Term Truth Table is False (0) are what is referred to in Handbook of Logical Validity as Onto-Monistic Proposition Types. Non-Monistic Universally Quantified Propositions such as 'All .W. is .V. (∀[.W.→13.V.])' and 'No .W. is .V. (∀[.W.↓07.V.])' in which Row Four is True (1) describe ordinary Sets of Objects in the World. Onto-Monistic Proposition Types which are Sound, however, are True for all Possible Worlds.
This Argument is proved by the following Venn Diagram:
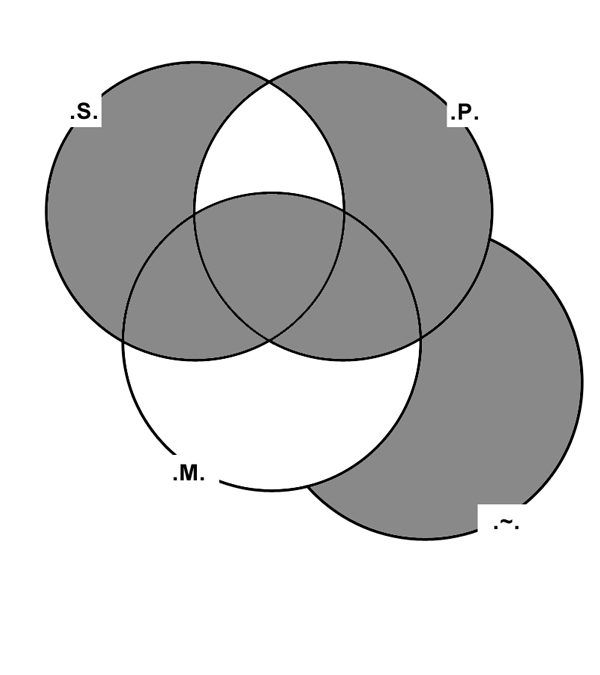
In Syllogistic form, this Argument is written:
∀(.M.⊗06.P.),
∀(.M.⊗06.S.);
_________________________
∴[∀(.S.≡09.P.).
Within the schema of Handbook of Logical Validity, this Argument Form is referred to as Universal Quantifier Argument: 06,06,09; Figure III.
Example of a Mixed Quantifier Syllogistic Calculus Argument Form.
Consider the following Formally Valid Argument:
∀(.Canines.→13.Mammals.),
∃(.My pet dog Rover.⊆12.Canine.);
_______________________________________
∴[∃(.My pet dog Rover.⊆12.Mammal.)].
This Argument is proved by the following Venn Diagram:
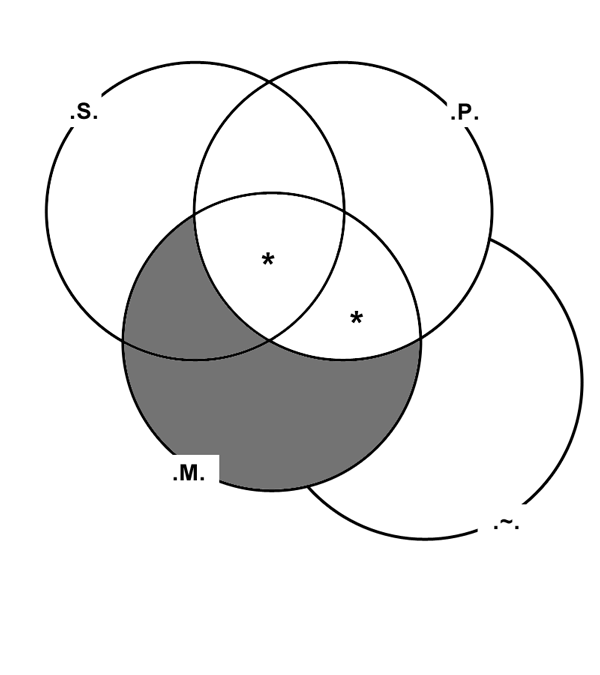
In Syllogistic form, this Argument is written:
∀(.M.→13.P.),
∃(.S.⊆12.M.);
________________________
∴[∃(.S.⊆12.P.)].
It is important to note that in this case the [∃(⊆12)] Truth-Functional Operator (TFO) cannot be empty. In other words, at least one member of this Set must exist (In this case 'My pet dog Rover').
The "All .S. is .P." [∀(→13)] TFO thus is slightly different from the [∃(⊆12)] TFO.
Another way of stating the '⊆12' TFO is "Each .S. is a .P." or ".S. is a Proper Subset of .P."
The reason that the "⊆12" TFO has not been explored by the prior Logic is the seemingly unaesthetic quality of being identical to the Truth Values of the Subsequent Proposition Type. Yet there are many other Interpretations we can place on the "⊆12" TFO.
The Truth Table for the "⊆12" TFO reads 'TTFF'; while the Truth Table for the "→13" TFO reads 'TTFT' (1100 Base Two = 12; and 1101 Base Two = 13).
Within the schema of Handbook of Logical Validity, this Argument Form is referred to as Mixed Quantifier Argument: 13,12,12; Figure I.
Example of a Propositional Syllogistic Calculus Argument Form.
Let ".L." stand for "Antecedent Set."
Let ".H." stand for "Subsequent Set."
Then, consider the following Formally Valid Argument:
"No .L. is .H." IS CONTRADICTORY TO "Some .L. is .H."
"All .L. is .H." IS CONTRARY TO "No .L. is .H."
__________________________________________________
THEREFORE, IF "All .L. is .H." THEN "Some .L. is .H."
This Argument is proved by the following Venn Diagram:
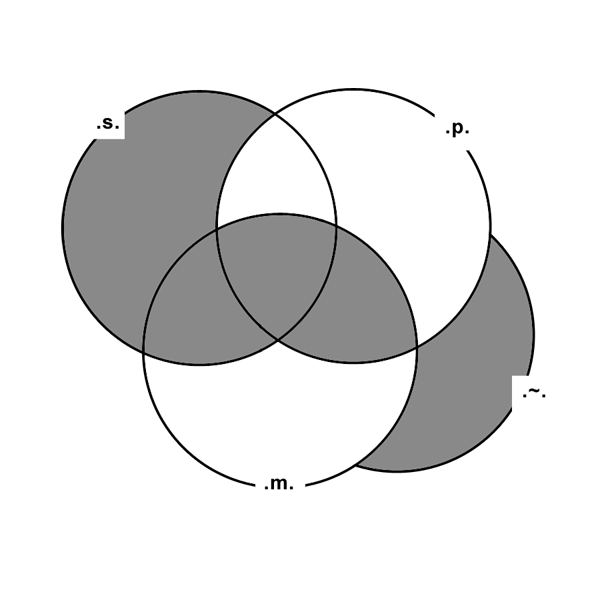
In Syllogistic form, this Argument is written:
(.m.⊗06.p.),
(.s.↓07.m.);
________________________
[∴(.s.→13.p.)].
Within the schema of Handbook of Logical Validity, this Argument Form is referred to as Propositional Argument: 06,07,13; Figure I.
Explorations on the Frontiers of Theoretical Science!
The illustrations on this page are only three of the 1,248 possible Venn Diagrams of Deductively Valid Syllogistic Argument Forms to be found in Handbook of Logical Validity. The result is an exponential expansion of established Argument Forms, which takes the 15 Categorical Syllogisms of the Classical Theory as a limiting case.
If you are experiencing difficulties understanding the ideas of this website, consult the "Elementary Logic" page.