Banner
Home HYPERMETROPHIA Handbook of Logical Validity Elementary Logic About the Author Contact the Author Buy the Books

A Brief Course in Elementary Logic

The History of Logic as a Theoretical Science

Logic was invented as a Theoretical Science by the ancient Greek philosopher Aristotle, in his book The Organon. Aristotlean Logic recognized four Proposition Types and tested for 256 permutations of Argument Forms, of which 24 were considered to be Formally Valid (Later Logical Theory abandoned nine of these Valid Argument Forms).

During the late 18th century, the German Philosopher Immanuel Kant introduced the notion of Synthetic a priori Propositions, which he defined as "Concepts which are constructed in intuition." Some a priori Synthetic thought processes known in Kant's time were Euclidean geometry and the laws of Mathematics, such as the Fluxions of Isaac Newton. Kant was famous for lamenting that, during the two millenia since Aristotle, "Logic has not taken a single step forward."

In the 19th Century, steps forward in Logic were taken by thinkers such as George Boole, Friedrich L. G. Frege, and John Venn. Certain Truth-Functional Operators were introduced, such as 'CONJUNCTION' (∧08) as well as 'INCLUSIVE DISJUNCTION' (∨14). The Universal Quantifier (∀) and Existential Quantifier (∃) were developed, and Venn Diagrams were invented. Of the 256 permutations of Argument Forms tested for by Classical Syllogistic Theory, 15 are found to be Formally Valid by Venn Diagram.

Renowned examples of Categorical Syllogisms are: "Socrates is a Man, All Men are Mortal; Therefore, Socrates is Mortal" (Valid). Or, "Socrates is a Man, Socrates wears a beard; Therefore, All Men wear beards" (Fallacy).

Classical Syllogistic Theory contains four Categorical Proposition Types (Well-Formed Formulae):

About the Sixteen Truth-Functional Operators (TFO's)

If you take two Logical Concepts, each of which could either be True or False, and combine them; then the total number of permutations of the Truth or Falsity of these combinations equal precisely sixteen. A logical concept could be either a Category (Set) or a Complete Proposition (Sentence).

In the past, logicians have restricted their attention to only several of these Truth-Functional Logical Connectives. Most persons are familiar with such Boolean Operators as 'IF-THEN' (Material Implication), 'AND' (Conjunction) 'AND/OR' (Inclusive Disjunction) as well as 'NOT' (Negation). The other TFO's were deemed hitherto as "not logically interesting" enough to study in a systematic manner.

A Proposition is a complete thought. A Category is a Set of Objects. For instance, "All primates are mammals" is a Categorical Proposition that connects the Sets "Primates" and "Mammals." The Category "Primates" by itself is not considered by formal logic to constitute a complete statement, yet when combined in this way with another Category "Mammals" this juxtaposition comprises a Complete Proposition.

A type of Categorical Proposition which has not been systematically contemplated by prior logicians is the statement: "Only Mammals are Primates." [∀(.Mammals.←11.Primates.]. However, the Categorical Proposition "No Mammals are Reptiles" [∀(.Mammals.↓07.Reptiles.)] has been considered by the earlier theory. An obvious Conclusion that can be derived from the two above Categorical Propositions is that: "No Primates are Reptiles."

Categorical Propositions and Compound Propositions

A Categorical Proposition is one single complete thought. A Compound Proposition is composed of two or more Complete Propositions.

The same Truth-Functional Operator that states "All primates are mammals" in a Categorical Proposition, can state "IF it is raining today, THEN (→13) water is falling from the sky." as a Compound Proposition. These types of Logical Connectives are already a part of the previously established Theory. So is the statement "No mammals are reptiles."

What has not been studied previously are statements such as ["Water is falling from the sky" BECAUSE (←11) "It is raining today"] or ["It is raining today" IS CONTRARY TO (↓07) "It is sunny weather today"].

In standard notation we refer to "Subject Categories" and "Predicate Categories" when discussing Categorical Truth-Functional Connectives. We refer to "Antecedent Propositions" and "Subsequent Propositions" when discussing Compound Propositional Truth-Functional Connectives.

Two Term Truth Table:

Left Column: Right Column: Row Number:
True True Row One.
False True Row Two.
True False Row Three.
False False Row Four.

 

Most, but not all, logic textbooks list the left column as: TTFF and the right column as: TFTF. However, the columns are here as left: TFTF and right: TTFF; for two reasons. One, it makes it easier to quickly handwrite the tables; and two, formatting the Tables as listed above allows us to consider these TFO's as Base Two numerals. The Right Column indicates Units and the Left Column indicates the Base.

For instance, 4 equals '100 Base Two'; or, 9 equals '1001 Base Two'. Thus, the sixteen binary Logical Connectives can be depicted as the Base Two Integers from '00' to '15.' That is the manner in which they are presented in the below table. "BASE2" stands for 'Base Two.'

Listing the Sixteen TFO's

Truth Values

In all these considerations:

Logical Variables

In all these considerations:

A Subscript from '00' to '15' is placed after the Symbol to denote its Base Two Integer.

The following table presents all of the sixteen Binary Logical Connectives:

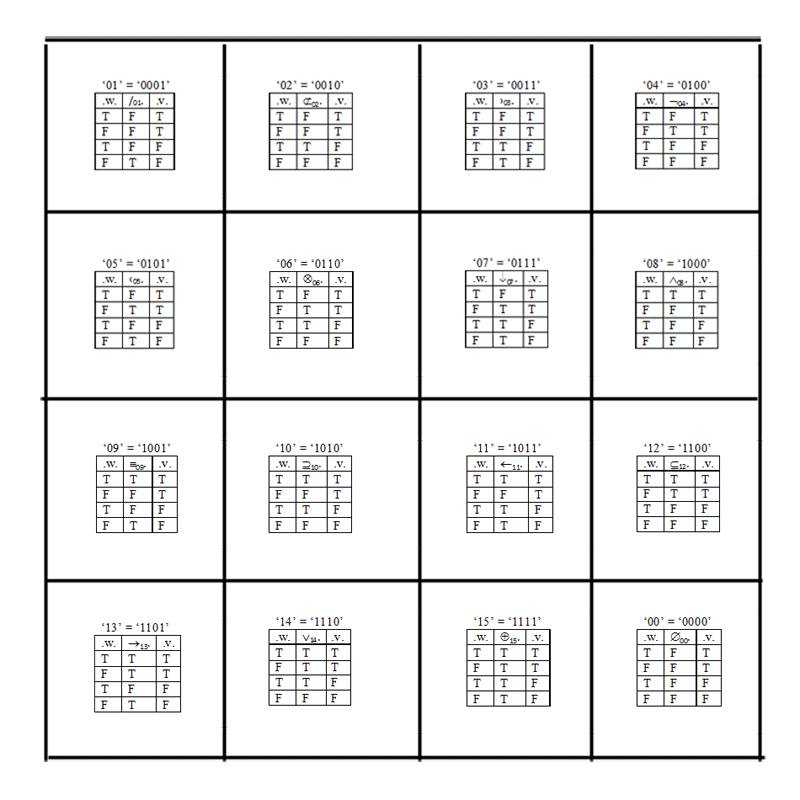
Sixteen TFO's

In a Two term Truth Table, the following Equalities hold:

A Note on Symbology:

In most Symbolic Logic textbooks, Antecedent Propositions are denoted by the letter p and Subsequent Propositions are denoted by the letter q, as in "If p, then q." However using the letter p would be confusing, because '.P.' already stands for "Predicate." So we have used '.W.' to stand for "Antecedent" and '.V.' to stand for "Subsequent."

Also, referring to the Right Column as "Consequent" allows only for the IF-THEN (→13) Statement, so we have changed this word to "Subsequent." The name "Subsequent," however, can be applied to the Right Column of any and all of the 16 Truth-Functional Operators.

The 64 Proposition Types

Let 'Term' represent both a Category and a Complete Proposition.

Let the expression:(.Ww.#16.Vv.) stand for any and all of the 16 TFO's listed above, where:

Upper case letters (.W., .V.) represent a Category.

Lower case letters (.w., .v.) represent a Complete Proposition.

Upper and lower case letters together (.Ww., .Vv.) represent a Term.

Logical Operators:

Let '.~.' stand for "Not-" or "It is not the case that:"

Let '∴' stand for "Therefore" or "It is the case that:"

Universally Quantified Proposition Types:

∀(.W.#16.V.).

Means: For every Object, .W. and .V., these Objects are related to each other Truth-Functionally.

Existentially Quantified Proposition Types:

∃(.W.#16.V.).

Means: There exists at least one Object such that .W. is related to .V. Truth-Functionally.

Individually Quantified Proposition Types:

Æ(.W.#16.V.).

Means: There exists precisely one Object which can be described Truth-Functionally in relation to the Sets .W. or .V..

Compound Proposition Types:

(.w.#16.v.).

Means: A combination of two Complete Propositions: .w., .v..

Three Term Truth Table

Let '.Ss.' stand for "Subject Term."

Let '.Mm.' stand for "Middle Term."

Let '.Pp.' stand for "Predicate Term."

Let 'r.' stand for "Row Number" (from 1 to 8).

The following table is a Three Term Truth Table used in the theory of Categorical Syllogisms.

 

.Ss. .Mm. .Pp. Row Number:
T T T r1.
F T T r2.
T F T r3.
F F T r4.
T T F r5.
F T F r6.
T F F r7.
F F F r8.

 

The Four Figures of Classical Syllogistic Theory

The following table describes the four Figures used in the theory of Categorical Syllogisms:

Figure I: Figure II: Figure III: Figure IV:
.M.#16.P.
.S.#16.M.
∴.S.#16.P. 		.P.#16.M. 
.S.#16.M.
∴.S.#16.P. 		.M.#16.P.
.M.#16.S.
∴.S.#16.P. 		.P.#16.M.
.M.#16.S.
∴.S.#16.P.

 

About Venn Diagrams

Venn Diagrams are a visual method of testing for Formal Validity in Logic. There are certain rules for which some regions are to be shaded (∀=False), some regions are to be left blank (∀=True), and for which a mark (∃=True) is to be placed within a region.

Regions within a Venn Diagram are also called Subsets. There are four Subsets on a Two Term Venn Diagram, and eight Subsets on a Three Term Venn Diagram.

Two Term Venn Diagram:

Two Term Venn Diagram

There exist 16 permutations of Truth-Functional Operators (TFO's) within a Two Term Venn Diagram.

 

 

Three Term Venn Diagram:

Three Term Venn Diagram

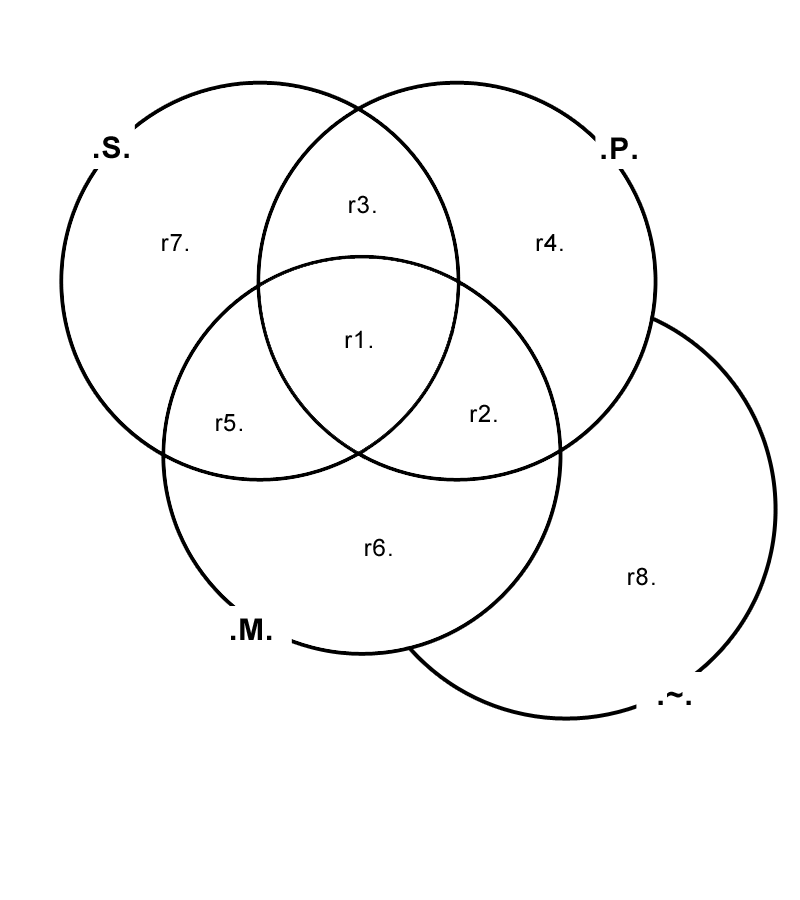
It is shewn in Handbook of Logical Validity that there are over 50,000 potential Argument Forms that can be derived from this Three Term Venn Diagram, of which 1,936 are found to be Formally Valid. Illustrations of these concepts are provided on the "Venn Diagram Examples" page.

Terms, Categories, and Propositions

It has been shewn in prior Logic textbooks that Venn Diagrams can be utilized to analyze Compound Proposition Types (complex sentences) as well as Categories. A Term is a Logical concept that denotes both Categories and Propositions (complete thoughts).

For instance, the Category (Set): "Mammals," by itself, is not a Complete Proposition; yet the statement: "All Mammals are Animals" is a Complete Proposition.

About Universally Quantified Onto-Monistic Proposition Types

In a Universally Quantified (∀) Proposition Type, a Statement is being made about all Objects in Existence. Row Four of a Two Term Truth Table is called "The Frame of Reference." Row 8 (r8.) of a Three-Term Truth-Table is called "The Universe of Discourse." When the Frame of Reference of a Universally Quantified (∀) Proposition Type is False (0), the Statement is being made about the entire World. Generally speaking Universally Quantified Onto-Monistic Proposition Types are the even numbered ones, in terms of their Base Two Numerology.

For instance, at the beginning of Tractatus Logico-Philosophicus, Ludwid Wittgenstein states: "The world is everything that is the case. The world is the totality of facts, not of things."

The Statement: "The world is the totality of facts, not of things" can be expressed Symbolically as:

[∀(.Facts.⊄02.Things)].

Since the "⊄02" Truth-Functional Connective is False (0) in the Frame of Reference (Row Four of the Two Term Truth Table) of this Universally Quantified (∀)Categorical Proposition Type, the Statement is being made about everything in Existence. Contrast this with, for instance, a statement such as:

"All Chairs are Furniture": [∀(.Chairs.→13.Furniture.)].

This is an example of what is called in Handbook of Logical Validity as a Non-Monistic Universally Quantified Proposition Type. Non-Monistic Universally Quantified Proposition Types refer to Sets of ordinary Objects in the World. Within these Types of Proposition, Row Four of the Two Term Truth Table (the Frame of Reference) is listed as True (1). The full details of this nomenclature is discussed in Handbook of Logical Validity. The entire purpose of this discussion is the ability to make what Immanuel Kant called "Scientific Metaphysical Statements."

Contraries versus Contradictories

The Universal Negative Categorical Proposition Type is called "Contrary," because both the Antecendent Set (Subjects) as well as the Subsequent Set (Predicates) can be False. The Universal Negative is denoted (↓07) or "No .S. is .P." (The integer '07' in BASE2 numerals equals '0111' (FTTT)).

Contrast '↓07' with the Contradictory Operator '⊗06' (The integer '06' in BASE2 numerals equals '0110' (FTTF)). In this case, both the Antecedent Set as well as the Subsequent Set are held to be False.

There are two Categorical Propositions that can be constructed from the '⊗06' Truth-Functional Operator, namely:

"∀(.S.⊗06.P.)" is a Universally Quantified (∀) Proposition Type, so it applies to the entire world. Therefore, this type of Proposition is considered an Onto-Monistic Statement.

"∃(.S.⊗06.P.)" is an Existentially Quantified (∃) Proposition Type, so it applies merely to one or more OBJECTS (Members of Sets) on its Frame of Reference.

It is proved in Handbook of Logical Validity that: If "No .S. is .P." is True, and at least one Member of the Subject Set exists as well as at least one Member of the Predicate Set exists; Then [∃(.S.⊗06.P.)] is the resultant Conclusion.

Stated Symbolically, this Argument runs:
[∀(.S.↓07.P.)],
(∃.S.),
(∃.P.);
∴[∃(.S.⊗06.P.)].

About the '⊄02' Truth-Functional Operator

Previous Logicians supposed that the Categorical Proposition "Some .S. is not .P." (Particular Negative) ought be denoted symbolically as "∃x(gx∧~fx)," meaning "There exists at least one x such that this x is a g and not an f." In this previous notation, "∧~" stood for "⊄02." With the recognition of all 16 TFO's as Logically significant, this newer notation for the '02' TFO seems to work much better than 'AND-NOT' (∧~). Also, treating the two Quantifiers (∀,∃) in relation to OBJECTS on a Frame of Reference obviates the need for the meaningless x's of the standard generally recognized notation.

(In BASE2 numerals, '0010' or 'FFTF' equals '02').

The Four Categorical Proposition Types of Classical Syllogistic Theory Stated Symbolically

Classical Syllogistic Theory contains four Categorical Proposition Types (Well-Formed Formulae):

Classical Syllogistic Theory tests for 256 permutations of Argument Forms, of which 15 are found to be Formally Valid by Venn Diagram. Contrast this with the Syllogistic Calculus of Handbook of Logical Validity, which tests for more than 50,000 permutations of Argument Forms, of which 1,936 are found to be Formally Valid. The Syllogistic Calculus contains 48 Well-Formed Formulae and takes the 15 Valid Arguments of Classical Syllogistic Theory as a limiting case.

The entire Logical System of Handbook of Logical Validity, called the Truth-Functional Calculus, contains well over 2,700 Deductively Valid Argument Forms, and incorporates the fewer than a hundred or so previously established Logical Argument Forms within itself.

For more information on this topic, go to the Handbook of Logical Validity page.

 

Back to the top of the page.