Banner
Home HYPERMETROPHIA Handbook of Logical Validity Elementary Logic About the Author Contact the Author Buy the Books

HYPERMETROPHIA: A Phenomenological Unified Theory of Fields

The word "Hypermetrophia" means "Far-sightedness." This is a 123 page book about everything (a Unified Field Theory). For more information about the concepts discussed on this page, consult: Elementary Logic.

An Innovation in Written Communication

This book is written in the form of what is called a 'Logically Perfect Language.' Certain protocols necessary for the intersubjective transmission of English vernacular prose; such as the use of definite articles, prepositional phrases, subordinant clauses, et cetera; are abolished within this Logically Perfect Language.

These literary artifacts are replaced by Truth-Functional Categorical as well as Propositional Connectives, thus eliminating the need for such ambiguities and idiosyncrasies of colloquial English prose.

Structure of HYPERMETROPHIA

Within the Theory, there are twenty-four Fields within four Quadrants. The entire structure is composed of 544 words. These words are considered 'Names' given to 'Sets of Logical Objects.' Two Names are combined to form a Categorical Proposition. A Categorical Proposition is considered by the Theory to constitute a 'FACT.' Categorical Propositions are connected into Compound Propositions. The resulting narrative is composed of a sentence that is 544 words long. The Categorical Propositions are placed within the framework of what are referred to as 'Coitads.'

About the 'Coitadology'

The word 'Coitad' is a type of acronym which stands for:

The word 'Coitadology' is defined as "The study of Coitads."

There are six types of Coitad:

There are two types of Dodecahads and two types of Hexad, which are called Left-Handed and Right-Handed. Thus, there are:

In the Theory of the Coitadology, generally speaking, terms are defined as one word Categories. The Coitadology is composed of a Self-Recursive structure that allows the same Conclusion to be derived from two separate Sets of Premises. The Coitadology, generally speaking, restricts itself to the Classical Syllogistic Case, containing the four Categorical Truth-Functional Operators as Well-Formed Formulae, with the exeption of the Quadrad.

For more information about the Logical framework behind these investigations, go to the Elementary Logic Page.

A Resolution of the Wave-Partical Duality?

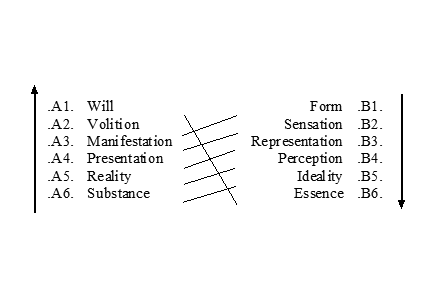
Consider the following Left-Handed Dodecahad:

Physics Duality

What is 'True for all Possible Worlds?'

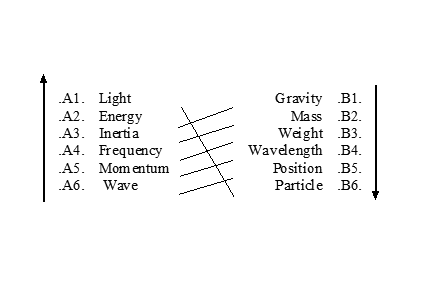
Consider another Left-Handed Dodecahad:

Metaphysics Dodecahad

The Universal Quadrad:

Universal Quadrad

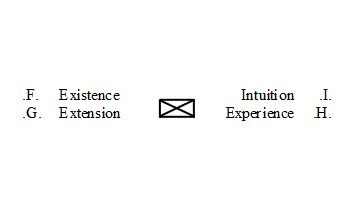
Truth-Functonal Significance of the Universal Quadrad

Consider the following Universally Quantified Proposition Type:

∀(.W.⊗06.V.).

The TFO "⊗06" means ".W. is Contradictory to .V." This TFO is also referred to as "Exclusive Disjunction."

The Two Term Truth Table for the '06' TFO lists Row Four as False. With some other Universally Quantified (∀) Proposition Types such as 'All .W. is .V.[∀(.W.→13.V.)]' and 'No .W. is .V. [∀(.W.↓07.V.)]', Row Four of the Two Term Truth Table is True.

Universally Quantified (∀) Proposition Types in which Row Four of a Two Term Truth Table is False are what is referred to in Handbook of Logical Validity as Onto-Monistic Proposition Types. Non-Monistic Universally Quantified Propositions such as 'All .W. is .V.(→13)' and 'No .W. is .V.(↓07)' describe ordinary Sets of Objects in the world. Onto-Monistic Proposition Types, however, if Valid, are True for all Possible Worlds.

The Universal Quadrad stated Truth-Functionally

The two following Logical Relations are held to hold for all possible worlds:

These are two instances of what are called by the Theory "Onto-Monistic Dyads."

Examples of Pentads

The Fluxions Pentad:

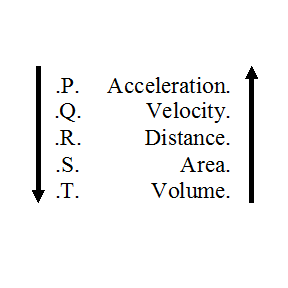
Fluxions Pentad

The Geometrical Pentad:

Geometrical Pentad

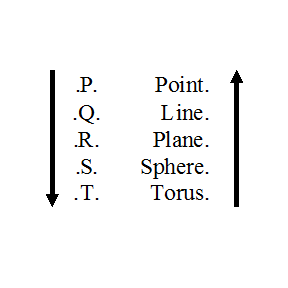
Structure of the Pentad

Axioms of the Pentad

Forward Set, Let:
Backward Set, Let:

Conclusions of the Pentad

Therefore, the five following Conclusions can be derived:

These conclusions can be proved by two separate sets of premises.

For instance, the following Compound Proposition is proved by the Structure of the Pentad:

[IF (All .Point. is .Line.) AND (∧08) (Some .Plane. is not .Line.)
THEN (→13)[∴(Some .Plane. is not .Point.)]
BECAUSE (←11) (Some .Line. is not .Point.) AND (∧08) (All .Line. is Plane.)].

This is one example of how, using the Pentad Structure, the same conclusions can be drawn from two separate sets of Premises. This example also shows how Categorical Propositions can be interspersed within Compound Proposition Types.

Within the Classical Syllogistic notation, the two Syllogistic Forms of the Pentad are of Mood and Figure: AOO-2 and OAO-3.

Left-Handed Dodecahad Structure

Axioms of the Left-Handed Dodecahad

Left Side, Let:
Right Side, Let:
Across Set, Let:

Conclusions of the Left-Handed Dodecahad:

Therefore, the six following Conclusions follow from the Axioms:

These conclusions can be proved by two separate sets of premises.

Example of a Left-Handed Dodecahad Conclusion:

For instance, the following Compound Proposition is proved by the Structure of the Pentad:

[IF (All .Position. is .Particle.) AND (∧08) (No .Wave. is .Particle.)
THEN (→13)[∴(No .Wave. is .Position.)]
BECAUSE (←11) (No .Momentum. is .Position.) AND (∧08)
(All .Wave. is .Momentum.)].

This is one example of how, using the Left-Handed Dodecahad Structure, the same conclusions can be drawn from two separate sets of Premises. This example also shows how Categorical Propositions can be interspersed within Compound Proposition Types.

The Categorical Proposition "No .Wave. is .Particle." (∀[.A6.↓07.B6.]) is an example of what is called a 'FACT' by the Theory. Likewise, another instance of a FACT is the Cateorical Proposition "Some .Plane. is not .Line." (∃[.R.⊄02.Q.]) of the Geometrical Pentad.

Within the Classical Syllogistic notation, the four Syllogistic Forms of the Dodecahads are of Mood and Figure: EAE-1, EAE-2, AEE-2 and AEE-4.

All of the fifteen Categorical Syllogisms of Classical Theory which are found Formally Valid by Venn Diagram are listed in HYPERMETROPHIA on page 107.

Example of a Right-Handed Dodecahad

The Mathematical Dodecahad:

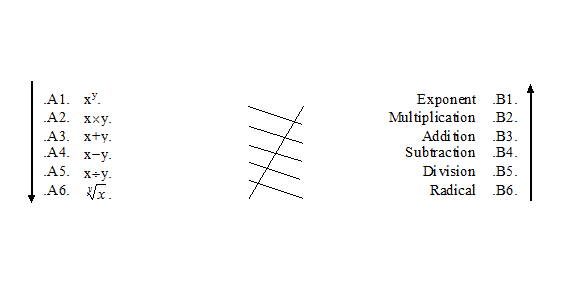
Example of a Right-Handed Dodecahad

Generally speaking, a Left-Handed Dodecahad is composed of six Dyads, while a Right-Handed Dodecahad contains two Hexads.

A 'Logically Perfect Language'

In HYPERMETROPHIA, the World Picture of Human Thought is divided into 544 Sets of Logical Objects. These Logical Objects are assigned Names. Names are treated as Categories, which are by definition Sets of Logical Objects. Two Categories are combined to form a Categorical Proposition. Categorical Propositions are considered by the Theory to constitute FACTS. These FACTS are then connected to each other by the Propositional Truth-Functional Operators (TFO's) to form Compound Propositions. These Compound Propositions are arranged within a hierarchy to compose a language made up of Categories only. The resulting structure is one Sentence which is 544 words long.

The phrase "Logically Perfect Language" was coined by the 20th Century British Logician and Philosopher Bertrand Russell, in his introduction to the book Tractatus Logico-Philosophicus by the 20th Century Austrian Logician and Philosopher Ludwig Wittgenstein. It is interesting to note that neither Wittgenstein nor Russell actually attempted to write in a Logically Perfect Language. To my knowledge, HYPERMETROPHIA is the only such attempt made thus far towards the description of the World using this Methodology.

A Logically Perfect Language can also be called a Mathesis Universalis. It is clear that the most obvious path towards "Metaphysics as a Strict Science" is a Logically Perfect Language composed of Universally Quantified Onto-Monistic Proposition Types (Onto-Monistic Propositions are discussed on Elementary Logic, at the bottom of the page).

Russell was also famous for posing the riddle: "The Barber shaves all those who do not shave themselves. So who shaves the Barber?" For an explication of this paradox, visit the Venn Diagram Examples page.

To read HYPERMETROPHIA in its full form, simply go to the Buy the Books page, and order a copy!

 

Back to the top of the page.